To FootIn a system where a primary body and a secondary body are gravitationally bound in circular or elliptical orbits, and there are no other significant gravity gradients, there are five co-rotating locations, the Lagrangian or Lagrange Points L1 to L5, in which a particle of negligible mass is in equilibrium. Only L4 and L5 can give stable equilibrium. Commonly, circular orbits are considered.
Ignoring the rest of the Universe, the entire system revolves at a constant angular velocity around its centre of mass (the barycentre).
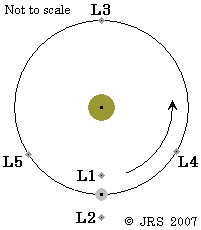
L1 lies between the two bodies; L2 and L3 are on extensions of a line between the bodies. They are always unstable positions, but spacecraft can readily be maintained at or near them.
L4 and L5 are to the sides, each forming an equilateral triangle with the centres of the two bodies. If the secondary body is much lighter than the primary body, L4 and L5 are stable positions for the particle.
The Points are named after Joseph-Louis, Comte Lagrange (1736-1813), an Italian-French mathematician who predicted L4 and L5 in 1772. L1, L2, and L3 were discovered by Euler. The fuller treatment by Lagrange, in Essai sur le problème des trois corps, includes L4 and L5.
Asteroids at Lagrange points were first observed early in the 20th century, in the Sun-Jupiter system, and named after heroes of the Iliad.
The Roche Lobes of primary and secondary meet at L1; their boundaries are surfaces of equal quasi-gravitational potential. L1, L2 and L3 seem to be saddle-points of potential.
On this page, upright letters are used for geometry, and italic letters for physical quantities. Thus 'm' is the location of the secondary body, and 'm' is its mass. It is assumed that the general nature of the phenomena is not affected by slight orbital ellipticity.
Here, I have in mind mainly the Earth-Moon system, but Sun-Earth and Sun-Jupiter Lagrange Points, for example, are also significant.
Approximately, the Earth's radius is 6400 km, the Moon's radius is 1600 km, and their separation is 384400 km varying by ±5.5%. The barycentre is about 1600 km below the Earth's surface.
At the Lagrange points, the gravitational forces are not balanced. They jointly provide the centripetal force necessary to maintain a particle at a constant relative position in the rotating system.
Some sites say that L1 and L2 are equidistant from the secondary body, which is only approximately true.
Many sites have put L3 at a greater distance from the centre of the primary than the secondary is, though actually it is at a slightly smaller distance. But it is correct to say that L3 lies outside the orbit of the secondary. Some draw L3 unreasonably near to the primary.
At least one site has said that L4 and L5 lie on the orbit of the secondary; but they actually lie a little outside it.
When the secondary is considerably lighter than the primary, the barycentre can be approximated by the centre of the primary, and L3, L4 and L5 are then at about the same radius as the secondary.
Page 126 of "The High Frontier", by Gerard K O'Neill, (c) 1976 (you
don't own it? My copy was £0.95 new in 1978) has a
clear diagram, equivalent to that here.
It shows L3, Earth, L1, Moon, L2 in that order in a straight line. L3, L4 and L5 are in the Moon's orbit, with L3 being opposite to the Moon and L4 and L5 being 60° away from it.
Generally, L4 leads, L5 trails; most other references agree.
(However, Henry Spencer once said that astronomers preferred the order L1, Earth, L2, Moon, L3; again L4 leads, L5 trails. Encyclopaedia Britannica 15th Edn shows L1, secondary, L2, primary, L3 and shows L4 lagging, L5 leading.)
As at 2007-02-02, Wikipedia had L3 further from the primary than the secondary is : that seemed wrong; to thar approximation, it should have been on the circle. Changed by 2007-02-07. It is interesting to look at corresponding diagrams in pages for different languages.
Balance of Gravitational Fields
Ignore corrections for the Sun's field and the motion of the Earth-Moon barycentre, and treat orbits as circular.
There is a point H between L1 and Moon at which there is, from Earth and Moon, no net gravitational force. It is at M / Q2 = m / q2 where Q+q is the Earth-Moon separation, D. As M ≈ 81×m, Q ≈ 9×q and H is about 10% of the way from Moon to Earth.
An unpowered body at H will not be changing its velocity but will be stationary or move in a straight line. But H itself moves in a circle, so the body and H cannot stay together.
Conversely, the net pull of the Earth and the Moon will, at L1, hold an unpowered body in a circular orbit with a period of one relevant Month. The body will remain at L1.
In calculating the location of any of the five Lagrange Points of a general two-body system, it is absolutely essential to include the effects of orbital motion around the centre of gravity - the barycentre - of the system. There is no "balance of gravitational fields" at any of the Lagrange Points.
In fact, unless the primary and secondary bodies have similar masses, an object at any of the Lagrange Points is basically orbiting the primary body, but in a manner modified slightly - in distance and stability - by the gravitational field of the secondary body.
At the Lagrange Points, the gravitational forces acting jointly provide the centripetal force which is needed to maintain a particle with the correct angular velocity in a circular path.
It seems to me that, in respect of L3, several other authors have
misrepresented the results of calculations, putting it too far out. L3
is slightly further from the barycentre than the secondary is, but it is
slightly nearer to the primary than the secondary is. Also, it is clear
that L4 and L5 must lie outside the orbit of the secondary, but they are
often said to lie on it.
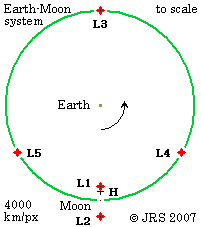
The diagram on the left is to scale for the Earth-Moon system. The barycentre is taken as fixed and the co-ordinates are non-rotating.
In the following detailed scale diagram, the sizes of Earth (M) and Moon (m) are in mutual proportion; but their mass ratio M:m has been changed from 81:1 to 9:1 in order to increase the differences between the various circles (at ratio 9:1, L4 and L5 are unstable; but they still exist). The densities have been scaled to give the correct relative diameters and to put the barycentre (C, Centre of Mass) at the same relative depth as for the real Earth and Moon. The yellow cross marks the fixed position of the barycentre. D is used for the distance between the centres of the two bodies.
The small fixed red circle shows the orbit of the centre of the Earth, and the fixed green circle shows the orbit of the centre of the Moon. Both of those orbits are centred on C.
The moving blue circle is centred on the Earth's centre, M; it is the set of points currently at a distance D from M.
The Lagrange Points are shown by red plus signs; the red crosses mark named geometrical points X, Y, Z. Points x, y, z exist corresponding to X, Y, Z but with M and m interchanged.
The outer thin fixed black circle is the path of L3; the inner one of L4 and L5.
L1 and L2, on the Earth-Moon line, are at similar, but different, distances from the centre of the Moon. The paths of L1 and L2 are of little interest, and so are not shown.
L3, L4, and L5 are all much nearer to, but are all outside, the Moon's orbit.
Note that L3 is outside the green circle but inside the blue one. Its path, centred on C, is shown by the outer thin black circle.
L3 is further from C than m is, and so is outside the Moon's orbit. L3 is at a smaller distance from M than m is, and so is inside the circle through Moon, L4 and L5.
Measured from the centre of the Earth, L4 and L5 are 60° from the centre of the Moon, and at the same distance D, thus forming two equilateral triangles, M4m and M5m.
The blue circle, on which L4 and L5 lie, is NOT the path of L4 and L5, though they remain on it. It is centred on the Earth's centre, and so is not fixed; it is epicyclic, and rolls around the green circle. Distances Mm and MX are equal.
The path of L4 and L5 is centred on C; it is shown by the inner thin black circle.
The field of M alone suffices to make m follow the green fixed circle around C. So a particle released with the same speed from Y, at the same distance from C but with more field from the nearer M plus some field from m, will move within the green circle. Therefore L3 is outside the path of the Moon.
Mm = MX
= D ;
Earth mass M, Moon mass m
Gravitational field on Moon is
GM÷Mm2
= GM/D2
balancing ω2×Cm
Gravitational field on Earth is
Gm÷mM2
= Gm/D2
balancing ω2×CM
Gravitational field at X is
GM÷MX2
+ Gm÷mX2
=
GM/D2 + Gm/4R2
Centrifugal effect at X is
ω2×CX
=
ω2×(CY+YX) =
ω2×Cm
+ ω2×CM×2
=
GM/D2 + 2Gm/D2
which is greater by 1.75Gm/D2.
Therefore L3 is nearer to the centre of the Earth than the Moon
is.
If the mass of the Moon were to tend towards zero, the yellow dot would move onto the black one and the red circle would shrink to zero; all of the large circles would correspondingly merge, and L1 and L2 would move into the Moon. The five Points would occupy four locations on the combined circle.
For equal masses in orbits of diameter D, corresponding Points are : L1 is central, L2 and L3 are at radius 1.198×D, L4 and L5 are on the dividing plane at radius D×√3/2 = 0.866×D.
Objects residing at L1, L2, or L3 must necessarily be artificial. As yet, there are only natural objects at any L4 and L5 Points. For more, see List of objects at Lagrangian points and other Wikipedia pages. The Pluto-Charon L4 and L5 points are unstable (mass ratio about 10).
| Some Known Objects at Lagrange Points | |||
|---|---|---|---|
| Primary | Secondary | Tertiary | |
| Previously | |||
| L1 L2 | Sun | Earth | L1: ISEE-3 - became comet explorer |
| " | " | " | L1: Genesis - returned samples |
| L3 L4 L5 | |||
| Existing | |||
| L1 L2 | Sun | Earth | L1: SOHO solar observatory |
| " | " | " | L1: Advanced Composition Explorer (ACE) |
| " | " | " | L2: Wilkinson Microwave Astronomy Probe |
| " | " | " | L2: Herschel, Planck |
| L3 | |||
| L4 L5 | Earth | Moon | dust clouds ? |
| " | Sun | Earth | dust clouds, asteroids ? |
| " | " | Mars | L4: 1999 UJ7 |
| " | " | " | L5: asteroid 5261 Eureka, and others |
| " | " | Jupiter | The Trojan Asteroids (see below) |
| " | " | Neptune | L4: Some trojan asteroids |
| " | Saturn | Dione | L4: Helene |
| " | " | " | L5: Polydeuces (S/2004 S5) |
| " | " | Tethys | L4: Telesto |
| " | " | " | L5: Calypso |
| Proposed | |||
| L1 L2 | Sun | Earth | L1: Sunshade, against Global Warming |
| " | " | " | L1: LISA Pathfinder |
| " | " | " | L2: James Webb Space Telescope |
| " | " | " | L2: Gaia, Darwin |
| L3 | |||
| L4 L5 | Earth | Moon | Colonies, G K O'Neill - re-positioned |
Points L1, L2 and L3 are not stable. Halo orbits exist around them and are used. I am uncertain of their stability, but I've seen it said that stable halo orbits exist for L1 and L2 at least.
The existence of L1, L2 and L3 is obvious enough; their locations are calculated below. Note that the intermediate Lagrange Point L1 is not the place where the attractions balance; one must remember, for all Points, that the rotation about the centre of gravity of the system requires a net centripetal force.
It appears evident that L1, L2 and L3 are radially unstable.
No natural bodies can be at any L1, L2 and L3 points, though they could perhaps exist in halo orbits. There can be no Counter-Earth at L3; Venus would have a large effect there.
The angular velocity ω about the barycentre is the same for the Earth, the Moon and the five Lagrange Points. The centripetal force required for a mass m to circle at a radius D is mω2D.
The Moon (mass m) orbits the Earth (mass M) at a mean distance D ~ 384,403 km; and, approximately, M = 81.25×m. The gravitational force GmM/D2 is balanced by mω2D, from which ω2 = GM/D3 .
Let the distance between a Lagrange Point and the nearest body be L; let the mass of the particle be o.
To the first order, we can ignore the motion of the Earth's centre of gravity.
For a particle at the inner Lagrange Point L1,
oω2(D-L)
is balanced by
Go(M/(D-L)2 - m/L2) ;
substituting for ω2,
M(D-L)/D3 =
M/(D-L)2 - m/L2 .
Changing to units where D = 1, m = 1,
and multiplying by L2(1-L)2,
ML2(1-L)3 =
ML2 - (1-L)2
ML2 - 3ML3 + 3ML4 -
ML5 = ML2 - 1 + 2L - L2
ML5 - 3ML4 + 3ML3 -
L2 + 2L - 1 = 0 (Equation L1).
The solution for M = 81 is near L = 0.151272;
that gives ~58,137 km from the lunar centre. Thus the inner
Lagrange Point is somewhat further from the Moon than geostationary
orbit is from Earth.
If M is large, L will be small, and equation L1 reduces to 3ML3 = 1.
For a particle at the Lagrange Point L2 behind the Moon,
oω2(D+L)
is balanced by
Go(M/(D+L)2 + m/L2) ;
substituting for ω2,
M(D+L)/D3 =
M/(D+L)2 + m/L2 .
Changing to units where D = 1, m = 1,
and multiplying by L2(1-L)2,
ML2(1+L)3 =
ML2 + (1+L)2
ML2 + 3ML3 + 3ML4 +
ML5 = ML2 + 1 + 2L + L2
ML5 + 3ML4 + 3ML3 -
L2 - 2L - 1 = 0 (Equation L2).
The solution for M = 81 is near L = 0.168327;
that gives ~64,692 km from the lunar centre. Thus the farthest
Lagrange Point is somewhat further from the Moon than the inner one.
If M is large, L will be small, and equation L2 reduces to 3ML3 = 1.
For a particle at the Lagrange Point L3 behind the Earth,
oω2L
is balanced by
Go(M/L2 + m/(D+L)2) ;
substituting for ω2,
ML/D3 =
M/L2 + m/(D+L)2.
Changing to units where D = 1, m = 1,
and multiplying by L2(1-L)2,
ML3(1+L)2 =
M(1+L)2 + L2
ML3 + 2ML4 +
ML5 = M + 2ML + ML2 + L2
ML5 + 2ML4 +
ML3 - (M+1)L2 - 2ML - M = 0 (Equation L3).
The solution for M = 81 is near L = 1.001029.
Thus the third Lagrange Point, at ~384,716 km is ~395 km
further away from the centre than the Moon is.
If M is large, L will be near 1.0, so set L = 1+λ, use (1+λ)n ≈ 1+nλ and equation L3 becomes 12Mλ = 1.
These need checking - both algebra and figures in km. Program "Lagrange" will do it.
Likewise, with masses of 1.984×1030 kg and 5.98×1024 kg, and distance of 149.46×106 km :-
LAGRANGE.PAS www.merlyn.demon.co.uk >=2000-03-11 Major mass, Minor mass, Separation ??? 1.984E30 5.98E24 149.46E6 Iterate L1 : 0.009982 1491926 km Iterate L2 : 0.010049 1501921 km Iterate L3 : 1.000000 149460038 km
The latest version of that program is in lagrange.zip; it gives the same results.
Point raised in mail received 2009-08-04.
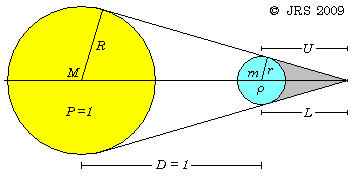
The length U of the umbra is Dr/(R-r). For M/m large and therefore L/D small, U is approximately r/R in units where D = 1.
Let the density of m be ρ, in units such that the density of M is 1. With also m = 1, (R/r)3 = ρM.
For large M, from First Approximation above for L2, we have 3ML3 = 1 with D = 1.
Therefore, U-3 = ρM and L-3 = 3M, so that U = L for ρ = 3.
On this approximation, L2 is at the tip of the umbra if ρ = 3, and is within the umbra if the secondary is less than three times denser than the primary, in the limiting case of a large ratio between the masses.
Therefore, on the large mass-ratio approximation. Sun-Earth L2 is somewhat outside the solar umbra (ρ ≈ 5.515/1.408 = 3.917). But Earth-Moon L2 is well within the umbra of earthshine (ρ ≈ 3.346/5.515 = 0.607), so it is not visible from anywhere on Earth.
The exact calculator below determines L from M, in real units. From that is now determined, for any given mass ratio M, the value of the density ratio ρ for which U = L and therefore L2 is at the tip of the umbra. R/r = (L+1)/L and (R/r)3 = ρM → ρ = ((L+1)/L)3 / M
This is expressed for Earth-moon L1, L2 and L3, but applies to all systems.
L4 x
/ \
/ \
/ \
/ \
/ \
/ L5 \
/ | \
/ V \
/ \
/ \
/ CoG \
|<---------L3--------->|/ | |<-L1->|<-L2->|
--x----------------------O-----+------------x------o------x--
|<-c->| |
|<-----------D----------->|
o M o m o
Masses : M is Earth, m is moon, o are particles at L1 L2 L3.
CoG is the Centre of Gravity (barycentre) of the Earth-moon system,
the centre of all rotation. L4 and L5 are at D from M and m.
CoG: c = mR/(M+m)
Earth: Mω²c = GMm/D²
(Moon: mω²(D-c) = GMm/D²)
L1: oω²(D-c-L) = GMo/(D-L)² - Gmo/L²
L2: oω²(D-c+L) = GMo/(D+L)² + Gmo/L²
L3: oω²(L+c) = GMo/L² + Gmo/(D+L)²
These equations cannot be simplified to the extent that the earlier ones were; but they can easily be iterated to a solution :-
LAGRANGE.PAS www.merlyn.demon.co.uk >=2005-04-28 Major mass, Minor mass, Separation ??? 81 1 1 Using CofG as centre of motion - c = 0.012195 : Iterate L1 ... 0.151109 Iterate L2 ... 0.168048 Iterate L3 ... 0.992886 + c → 1.005081
And :-
This includes results associated with L4 and L5, using the 60° geometry below.
Computation of L2 corrected, 2005-04-28.
Computation of density ratio ρ for L2 at umbra tip added,
2009-08-08, needs checking.
M/m 1e0 1e1 1e2 1e3 1e4 1e5 1e6 1e7 ie8 ρ 14.4 5.85 4.06 3.45 3.12 3.09 3.04 3.02 3.01
2007-01-05 : Wiki : For M >> m, L1 ≈ L2 ≈ Hill Radius - verify, expand.
Points L1 and L2 can be used as "gateways" for very low energy transfer orbits - see in Baez - which can be better than Hohmann orbits.
To see that L4 and L5 exist for a particle, it is sufficient to consider, as below, the balance of centrifugal and net attractive forces in [rotating] barycentric coordinates. The 60° is not measured barycentrically; L4 and L5 form an equilateral triangle with the primary and secondary bodies, for any mass ratio.
Determining the stability of L4 and L5 is beyond my present scope. There is a page at NASA GSFC.
There are in general stable regions around L4 and L5.
I have read that L4 and L5 in the Earth-Moon system are actually not stable points, because of lunar eccentricity and solar perturbations. I have read that stable orbits around them should exist, and that dust there may have been observed (Kordylewski clouds).
When stable, the Lagrangian points L4 and L5 of a system are termed Trojan Points. The original Trojans are in the Sun-Jupiter system. Around the Jovian L5 position are many asteroids named after Trojan heroes from Homer's Iliad, with one Greek among them; and around the Jovian L4 position are Greek heroes, with one Trojan. The misplaced are Hector of Troy and Patroclus (slain by Hector) of Greece.
The Earth, the Moon, and L4 (or L5) form an equilateral triangle rotating about the Earth-Moon centre of gravity. A surprisingly simple geometrical argument shows that the attraction on a particle at L4 (or L5) is correctly directed for this, and that it is of the correct magnitude.
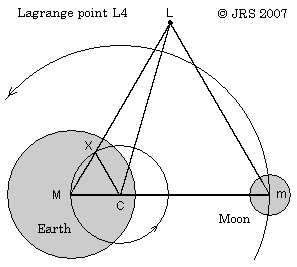
For a diagram, one needs to reduce the mass difference. Draw an equilateral triangle MmL (pyramid, L at top, M at left). Mark the centre of gravity of M and m on line Mm as C, so that M×CM=m×Cm. Draw LC. Through C, draw CX parallel to mL, with X on ML. X clearly divides ML in the same ratio as C divides Mm : MC=MX=CX, Cm=XL.
As ML=mL, the two field components on L, from M and m, are proportional to M and m. One sees that LXC is a triangle of fields, so that the net gravitational field on L from M and m is indeed directed towards C; and also that the fields on L, m, and M are proportional to LC, mC and MC, as is required to provide centripetal forces for the three bodies rotating in unison. Note that LC > mC >> MC.
The above argument appears as applicable to elliptical orbits as to circular; the orbit of L is at 60° from that of m.
The argument is independent of mass ratio; for two equal masses, a particle can orbit (unstably) at two points on the bisector, 60° from each mass, and √3 times as far from the centre.
Query : Is there a simple purely-geometrical construction for the case of three non-negligible masses?
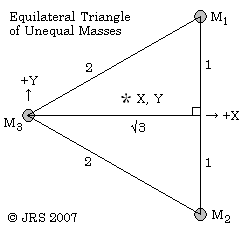In this case, L-notation does not apply.
Try an equilateral configuration. Put M3 at the origin, and M1 & M2 at X = √3 ; let the barycentre (marked *) be at X, Y.
|
For the barycentre : consider balancing the
M1 M2 M3
plane on a pin in the Z direction at (X,Y) :-
X : (M1+M2)(√3 - X)
= M3 X
|
For the field acting on M3 :- Fx = (M1+M2) √3 / 2 = ½ (M1+M2+M3) X Fy = (M1-M2) / 2 = ½ (M1+M2+M3) Y
Therefore the field on M3 is proportional to the distance to the barycentre and is directed towards it. One can do the same calculation for M1 and M2 by moving and turning the co-ordinate system.
So three bodies in equilateral formation can be in circular orbits around their barycentre, since the net force on each is directed to the centre and proportional to the distance from it.
Their stability is another question.
For a particle, L4 and L5 are stable only if the primary/secondary mass ratio exceeds about 24.96; they are stable, though less so, for matching elliptical orbits.
JH has written :- In order to be stable, the masses of the three bodies must obey the formula: 27*(m_1*m_2 + m_2*m_3 + m_3*m_1) < (m_1 + m_2 + m_3)^2; and, later, I got it from an article in Volume 5 of "What's Happening in the Mathematical Sciences" by Barry Cipra.
For the border of stability when the third body is a particle :-
27(m1m2
+ m2m3
+ m3m1) =
(m1 + m2 + m3)2
Put m3=0 :
m12 - 25 m1m2
+ m22 = 0
m1/m2 =
(25 ± √ (625-4)) / 2
= 24.9599 and 1/24.9599
For equal masses, put m1 = m2 = m3 = 1, and the comparison reduces to 27*3 < 3^2 and the configuration is clearly unstable.
The stability criterion can be given as (Orbital Motion, A.E. Roy, p. 138): mu = (1/2) - (23/108)^(1/2) , where mu is the reduced mass of the secondary body; that's 0.03852 = 1/25.96, i.e. primary mass is 24.96 times secondary mass.
For m_1=1, m_3=0 I get m_2 = 1/24.9599 for equality. For total mass 1 and m_1=1-u m_2=u m_3=0 that expression becomes 27 u (1-u) < 1 from which u = 1/25.9599 for equality. The difference of reciprocals is exactly 1.0, and corresponds to a mere difference in terminology.
The above stability conditions may be derived from "Routh's criterion".
Appendix, showing changes as mass moves from one body to the other : $lag-pts.htm.
Klemperer rosettes consist of many similar moons orbiting a planet or a point in one ring, or similar.
The neat stability equation boxed above shows that three bodies of equal mass are not stable.
SF authors show various related beliefs.
Other stable multi-body configurations have been found - AMS, A new solution to the three body problem - and more; Cris Moore, Gallery.