 To Foot
To FootHow far away from its planet can a moon be?
For a mathematical evaluation of the binding, one wants an analytic solution to the intractable three-body problem. Numerical simulation is therefore much used nowadays for this class of work.
This section is, for convenience, written in terms of the Sun-Earth-Moon system, and assumes circular orbits; but the principles can apply in other cases.
Let the primary mass be M, the secondary mass be m orbiting at distance R, and the test particle be at distance r from the secondary. The value of Newton's constant, G, will not be needed.
For the Sun-Earth-Moon system, M = 2×1030 kg, R = 150×106 km, m = 6×1024 kg, r = 400×103 km, approximately.
Someone wrote : The gravitational attraction between the Sun & the Moon is twice the attraction between the Earth & the Moon throughout the Moon's orbit. One can say that the opposite force which stabilizes the Moon has to be somewhere in the motions of the three bodies.
Remember that the Sun pulls both on the Earth and on the Moon.
The Sun's gravitational field at the Earth (GM/R2) is substantially equal to the Sun's field at the Moon. Thus the Moon appears just to orbit the Earth, even though, as shown in The Paths of Moons, its true path is mainly due to the effect of solar gravity.
At the Moon, the Sun's field is about double the Earth's; but to assess the binding, one needs to compare the field from the Earth at the Moon with the difference between the Sun's field at the Moon and the Sun's field at the Earth.
Differentiate GM/R2 and multiply by the Earth-Moon distance, getting -2GMr/R3. That reduces the "double" by a factor of -2r/R = -2×0.4/150. So the Moon's motion with respect to the Earth is dominantly due to the Earth's field with perturbation of about 1% due to the Sun's field gradient.
The collected mathematical works (Volumes 1-4) of George William Hill (1838-1914) can be read at Cornell.
The Hill Radius is rh = R(m/3M)1/3 ; that is (1/3)1/3 of the distance from the secondary at which the secondary and primary field gradients are equal.
Using ω2 = GM/R3 with the above, one gets that at the Hill Radius t√3 = T where t and T are the "month" and "year" respectively. Check!
With the above figures, the Hill Radius is 1.5×106 km (230 Earth radii); nearly 4 times the Moon's distance.
Since the change in the Sun's field at the Moon between New and Full is proportional to the size of the Moon's orbit, and the Earth's field obeys an inverse square law, the degree of binding is inversely proportional to the cube of the orbital radius.
The Sun's gravity gradient (GM/2R3) is matched by the Earth's (Gm/2r3) at r = R(m/M)1/3; that gives for the gradient match r = 2.16×106 km.
On 2000-06-08, in news:rec.arts.sf.science, Brian Davis wrote : Moons: you can get limits by assuming a moon's orbit will be ... inside about 1/3rd of the Hill radius ( a_hill = a_planet ( M_planet / (3 M_sun) )^(1/3)). ... while outside the Hill sphere it would be removed from its orbit by solar perturbations.
He has added, in E-mail, that the limit for a satellite orbiting in the opposite sense to its planet is about rh/2.
Let A and a be the diameters of the primary and secondary bodies, and Ρ and ρ be their densities.
(a) Densities :
M = πΡA3/6 ;
m = πρa3/6
(b) Newton :
GM/R2 = ω2R
= 4π2R/T2
→ R3/M = GT2/4π2
(c) Hill Radius :
rh = R(m/3M)1/3 →
(rh3/m) = (R3/M)×1/3
From (b) and (c), TH2 = T2/3 where T is the period of the Earth and TH can be called the Hill Period, in which an unperturbed moon at the Hill Radius would orbit the Earth.
From (a) and (c),
(rh/a)3 / ρ
= (Rh/A)3 / 3 Ρ
→
θ3 ρ
= 3 Θ3 Ρ ;
θ and Θ are the angular diameters of the
attractors as seen from the bodies orbiting them.
Thus a certain approximate ratio between the width of the Earth as seen from the Moon and the width of the Sun as seen from the Earth is critical, since the cube root of density is not much different for Sun and Earth, and for most pairs of bodies in the Solar System.
In fact, the density of Earth is (just) under 4 times that of the Sun; so from the Hill radius the Earth will look only about 10% smaller than the Sun.
As a moon can only orbit within about 1/3 of the Hill radius, one can deduce that, for any system resembling ours, a viewer on a moon will always see its planet as visually bigger than its sun.
The above all needs checking.
There should be an analogy with Roche here, too.
When two secondaries have very similar orbits around a common primary, one or both may have a "horseshoe orbit", reversing the relative direction of motion at each encounter. Example :- Janus and Epimetheus, two of the inner satellites of Saturn; ...?
The orbits are "horseshoes" only in rotating coordinates; in fixed space they are approximate circles.
Brian Davis has written - Assuming circular, co-planar orbits with close to equal-mass bodies, you will have horseshoe orbits if the separation is less than delta :-
where "mu" is the reduced mass..
There, "mu" must be the reduced mass of a secondary with respect to the primary, m/(M+m).
I'm told that for a small body to be in a stable circular orbit around a sun, it must not come within about 3.5rh of a planet.
I imagine that rh can be involved in considering the "shepherding" of rings by nearby moons.
The Horseshoe limit is presumably when the gravity gradient of the primary is matched, to within a factor of the order of unity, by the gravity gradient of one secondary at the other at what would otherwise be the closest approach.
The Roche limit is where the gravity gradient of the primary matches the gravitational cohesion of the secondary.
So there is a similarity, and the one-third power in the equation shown is to be expected (with moderate confidence).
Tide is caused by non-uniformity of an external gravitational field, generally in combination with relative motion, rotational or translational. A "moving" tide will always be associated with dissipation of energy.
For a body of density ρ and diameter d, with mass M proportional to ρd3, the gravitational field at a distance D is GM/D2. Therefore the differential field, which determines the tidal influence, is -2GM/D3. The tidal influence at D is therefore proportional to the density of the body, and to the cube of its apparent angular diameter d/D, only.
A person has a specific gravity near 1.0, not much less than that of most astronomical bodies. Therefore at most free-space locations in the solar system the tidal field strengths are much less than that of a nearby person would be.
I have read that : "The effect of tides is proportional to: Mr4 / mD3 where M = mass of inducing body, m = mass of subject body, r = radius of subject body, D = distance between the bodies.". That having the dimensions of distance, I suppose the effect to be the height of the tide on a homogeneous liquid body.
Now M = k Ρ R3, m = k ρ r3 ; the above becomes (Ρ / ρ)(R / D)3 r = (Ρ / ρ) θ3 r in which θ is half of the angular width of the inducer as seen from the subject body.
That seems very compatible with Roche breakup being related to ordinary tides; when the height of the tide becomes comparable with the size of the planet, the planet is coming apart.
Tidal energy dissipation generally causes the orbits and rotations of planets and moons to circularise and synchronise; inclinations may increase or decrease.
Sea-tides are mainly caused by the lunar gravity gradient (with a significant component from the solar).
There are generally two equally-spaced high tides per day in the open ocean, one occurring (more or less) when the Moon is highest; but the tides are about 40 minutes later each day, due to the Lunar Month.
The sea facing the Moon (being nearer) is attracted by the Moon more strongly than is the Earth as a whole, and the sea on the farther side is attracted less strongly than is the Earth as a whole. The sea therefore rises in two areas, under the Moon and opposite it; and falls in between. The Sun, the orbiting of the Moon, the rotation of the Earth, the presence of land, and dissipative effects combine to generate the complications that are actually observed.
"Spring" tides should occur when Earth, Sun, and Moon are substantially in line (Full & New Moon), so that the gradients reinforce; "Neap" tides should occur when Sun, Earth, and Moon form a right angle (First & Last Quarter). Eclipses only occur at Spring Tides. In practice, the tidal effect is delayed by a couple of days.
The Sun and the Moon match in apparent angular diameter, so comparison of their contributions to the sea-tide gives an estimate of the ratio of their specific gravities. Those are about 1.39 and 3.39 respectively, corresponding to a tidal field ratio of 41%.
The strengths of the lunar and solar components of the tidal field are affected by the monthly and yearly changes in the distance of those bodies from the Earth; and their orbital inclinations must also have some effect.
The gravity gradient of a large body can break up another nearby body.
As I recall, the conventional expression of Roche's Limit for a non-cohesive non-rotating satellite of a primary body is that the satellite will be broken up tidally if the centres are less than about 2.45 primary radii apart. The density-ratio dependence of this value is often forgotten.
Natural satellites of non-trivial size (including those of Mars) are always outside the Roche limit. Rings are inside it; their particles are small enough for cohesive forces to exceed tidal stresses.
On an astronomical timescale, asteroids frequently pass Earth at of the order of ten times the Roche distance. For a rubble-pile body, the tidal forces can disturb the surface material, thereby exposing fresh, "unweathered", paler, rock and visibly changing the colour - Abstract.
The paper by Édouard Roche (1820-1883), "La figure d'une masse fluide soumise á l'attraction d'un point éloigné", Acad. des Sci. de Montpellier, vol.1 (1847-50) p.243, was quoted with a later full calculation in Phil. Trans. Roy. Soc., 206A (1906) 161-248. That was reprinted in GH Darwin, Papers III (CUP, 1910) p.436 ff, which I saw long ago.
A Web search for the words of the subject of that paper finds much related information, and might lead to the paper itself. Google Books, searched for Edouard Roche masse soumise or the full subject, seems to have the whole work; but so far has shown me only in its three parts : Part 1 (p.243 ff), Part 2 (ibid p.333 ff), and Part 3.
There is also the Roche Lobe; "Roche Sphere" is another name for the Hill Sphere.
The following simple, approximate calculations may be of interest; each takes a simplified model (ideally, one should do a full deformation calculation for a liquid-drop secondary).
Further corrections are liable to be needed if the secondary is not small in comparison with its primary, or if it is rotating.
For a non-rigid body that breaks, as calculated below or otherwise, into two non-rigid pieces of whatever sizes, the same argument again applies to each piece. Thus, in the absence of any other significant forces, the whole lot will come apart. To be more exact, the piece that moved inwards will come apart, but the piece that moved outwards may move outside the Limit and so remain. But the vibration after break-up may ease some further dissolution
Consider throughout a large primary, radius R, density Ρ, and a secondary of size r, density ρ, at a distance d from the primary. M and m are primary and secondary masses.
For a given density, the internal gravity in the secondary is proportional to distance from its centre, independently of its radius; and the tide from the primary within the secondary follows the same law. Ignoring cohesion, the size of the secondary thus should not affect the distance at which the secondary comes apart. A hypothetical small rigid non-cohesive homogeneous sphere would break into planar laminae on crossing the critical distance.
The tidal stress on the secondary must be proportional to the primary mass, and hence to ΡR3, and inversely proportional to the cube of the distance (inverse square field, differentiated); the gravitational cohesive field of the secondary must be proportional to its density; the form of the Roche expression then follows as being :-
(d/R)3 = K (Ρ/ρ) or d = k R (Ρ/ρ)1/3
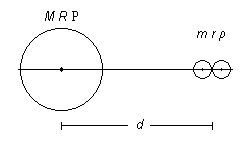
A two-sphere secondary resembles a liquid drop at the point of fission; so one can reasonably expect the true answer, apart from a constant factor near unity, for such a model.
Consider a secondary of two equal small spheres, radii r, touching, in-line with the primary. Will the spheres remain in contact?
Let a = 4π/3. Then the masses are
M = aΡR3 , m = aρr3 .
The attractive force between the secondaries[1]
is Gm2/(2r)2.
The attractive force between the large body and a small one at
d is GmM/d2; differentiate
this with respect to d to get -2GmM/d3,
multiply by the difference
in position, 2r, to get -4GmMr/d3.
These balance[2] when
4GmMr/d3 = Gm2/(2r)2
→ 16M/d3 = m/r3.
But
M = aΡR3 , m = aρr3 , so
16R3Ρ/d3
= r3ρ/r3 = ρ ; inverting,
(d/R)3 = 16 Ρ/ρ .
So d = 2.52 R (Ρ/ρ)1/3
; the result is about right.
Notes :-
[1] Approximately, as the field of a sphere is not homogeneous.
[2] Ignoring possible centrifugal effects.
We can see that equations for L1 & L2 (in
"First approximation", Gravity 4),
in the case of large mass ratio
M, which means small L, reduce to
3ML3 = 1 .
For primary and secondary, we have
M = (Ρ/ρ)(R/r)3 .
Express L as l/d, where l is the height of L1 & L2
above the centre of the secondary, and d is the separation
between primary and secondary; then we have
3ΡR3l3 /
ρr3d3 = 1 .
Now a particle inside the Lagrange distance will tend towards the
centre of the secondary, and one outside that distance will tend away
from it. Equating, then, l and r, we get
(d/R)3 = 3 Ρ/ρ ,
d = 1.44 R (Ρ/ρ)1/3 .
This gives d about 57% of that of the equal-sphere model, suggesting that the tendency is to break the secondary in two equatorially more than to evaporate the poles.
One can also calculate for the case of a primary, a secondary, and a loose pebble on the secondary at the point nearest to (or farthest from) the primary.
The primary field is GM/d2, its derivative is -2GM/d3, its change over r is -2GMr/d3.
The secondary field pulling the pebble down is Gm/r2.
Balance is at
Gm/r2 = 2GMr/d3
so rρ = 2R3Ρr/d3
→ (d/R)3 = 2 Ρ/ρ ;
d = 1.26 R (Ρ/ρ)1/3
.
If the secondary is in circular orbit, its rotation may well be tidally locked so that one side of it always faces the primary. The "centrifugal field" aids break-up.
At the equator, this field is ω2r in which ω is the angular rotation of the secondary and matches its orbital rotation, for which GM/d2 = ω2d , so the field is GMr/d3.
Balance is at Gm/r2 = 3GMr/d3
so
rρ = 3R3Ρr/d3
→ (d/R)3 = 3 Ρ/ρ ;
d = 1.44 R
(Ρ/ρ)1/3 .
This agrees with the Lagrange model.
The best value that I have seen for the Roche constant is 2.423, in Weisstein's Roche Limit.
David W. Knisely (dk84538@navix.net), in an interesting discussion, has pointed out that the limit can be expressed either as d = 2.423 r (M/m)1/3 , or as d = 2.423 R (Ρ/ρ)1/3 .
It follows that the Roche period does not depend in any way on the nature of the primary, but is inversely proportional to the square root of the density, ρ, of the afflicted secondary body itself.
Dimensional arguments permit this; Gρt2 is dimensionless.
From Low Orbit Time,
Low Period :
t = √ ( 3 π / (G Ρ) ) seconds;
so the period at the Limit
T = ( 3π / (G Ρ) )1/2 × (d/R)3/2
= ( 3π / (G Ρ) )1/2 ×
(2.423 × (Ρ/ρ)1/3)3/2
= ( 3π / (G Ρ) × (2.423 ×
(Ρ/ρ)1/3)3)1/2
= ( 3π / (G Ρ) × 2.4233 ×
Ρ/ρ )1/2
= ( 3π / (G ρ) × 2.4233 )1/2
= √( 3π × 2.4233 / G ) /
√(ρ)
~ = 1.417×106 / √(ρ)
seconds.
Remember to put the density, ρ, in
kg/m3.
The Moon's specific gravity is 3.39, which gives about 24300 seconds, or about 6h 46m. The period of Phobos is 7h 39m.
See also "Rotation of asteroids and planetary axial rotation theory", Barricelli, N A, in "Moon and the Planets", vol.27, Oct.1982, pp.179-185.
Use any distance units; the densities must be in kg/m3.
To first order, what difference if any does it make if the secondary is not homogeneous but consists of two unmixed fluids of different densities?
The outer limits of the icy particulate ring systems of the four major planets of the Solar System are near, but within, the Roche limit.
One must distinguish between natural particulate rings, found in astronomy (e.g. Saturn's) and artificial continuous rings, found in fiction (Niven, Clarke, ...).
It is absolutely clear that a rigid ring of negligible mass, whether or not spinning, and a massive, central, sun are a case of unstable equilibrium. The type of argument in Gravity of a Spherical Shell shows it, because gravity is inverse square, but areas become line segments.
But a set of point objects of negligible mass in a circular orbit around a massive, central, sun are assuredly in a very stable situation; and the same must be true of a "dense set" joined into a ring by massless, strengthless connections (e.g. with frictionless sliding and hingeing joints).
What happens in the intermediate case of a flexible, inextensible rope of negligible mass and proper orbital velocity - "Stringworld" ? I recall mention of a "suspension bridge without endpoints" - is there a simple treatment, akin to that above?
Or, indeed, an elastic rope - which should be more difficult to understand - RubberBandWorld ?
Or if the sliding, hingeing joints were lossy (but without static friction) ?
N.B. Larry Niven's Ringworld spins much faster than orbital velocity.
I'm told : Book "Satellites", University of Arizona Press, ed. Burns.
My thanks to Brian Davis of IUSB, IN, USA, for advice, particularly on Hill theory.