 To Foot
To FootWhile conventionally called velocities, these are really speeds. Orbital speed balances "centrifugal force" for a circular orbit. Escape speed for a location is the speed needed for an unpowered, unbraked object to be able to reach infinity from that location; it gives a positive kinetic energy matching the negative potential energy at that position.
Surface orbital velocity satisfies V2/r = g, so V = √(gr). Thus the orbital energy is 0.5mV2 = 0.5mgr ; and the escape velocity is √2 times the orbital velocity. For uniform acceleration at g, V2 = 2gs, so s = r/2 ; to attain orbital velocity with a horizontal acceleration of g (and an initial overall "weight" corresponding to g×√2) takes half a radian. Escape velocity takes a full radian.
So escape velocity from the surface would be attained by falling for one radius at one surface g.
Assume a diametrical tunnel in a spherical, homogeneous, atmosphere-free Earth. As an LEO satellite passes overfoot, drop a stone in the hole. It seems clear (below) that they will arrive at the other end of the hole simultaneously, and therefore that the "part-escape speed" to the surface from the centre is equal to LEO speed; hence the corresponding part-escape energy equals the LEO energy (per unit mass). Normal escape energy is twice LEO energy, so central escape energy is thrice LEO energy, and central escape speed is root three times LEO speed.
A photon is exhausted in escaping to infinity from the surface of a black hole. That suggests, classically, that mgr = ½mV2, i.e. g = ½V2/r. Now g = GM/r2, leading to r = 2GM/V2. That happens to agree with a reliable relativistic expression for the Schwarzschild radius - which is r = 2GM/c2.
Kepler's Three Laws of Planetary Motion - An Overview for Science teachers, by David P. Stern, GSFC.
Johannes Kepler (1571-1630) derived his three Laws from observations, in particular of Mars; they can be re-stated as :-
These apply in the case of two bodies interacting by an attracting force along the line of their centres, proportional to the product of their masses and inversely proportional to the square of their separation. The third Law applies among the secondaries of a given primary.
Kepler's Laws (K1 K2 K3) can be derived from the Laws of Motion and the Inverse Square Law. They can in part be obtained by simple arguments; for a full mathematical derivation, see for instance Erik Max Francis.
At any instant, the attracting centre and the velocity vector of the secondary define either a line or a plane, which contains the force vector. The motion therefore remains in that line or plane, which is part of the First Law and could have been called a Zeroth Law.
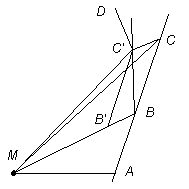
Following Newton : Let the massive primary be at M, and let the line ABC represent two small equal-duration elements of the constant-velocity path of the secondary that would occur in the absence of attraction. Triangles AMB, BMC have equal bases AB BC and a common height, thus the same area, proportional to the angular momentum about M.
Now consider the attraction represented by an impulse at B along BM, imparting velocity BB'; draw CC' equal and parallel to BB'; BC' then represents the second segment of the motion. Area AMB = BMC as before, and MBC = MBC' have a common base MB and equal height, so area BMC' = AMB and we have the equal-area rule K2.
Kepler's Second Law is a direct consequence of the conservation of angular momentum for the case of a body subject only to a force directed towards a fixed centre.
The angular momentum is the mass times the circular component of the velocity times the distance, whereas the area swept out in unit time is one-half times the distance times the circular component of the velocity.
Kepler's Third Law is easy for circular orbits, using simple algebra :- ω2r = (2π/T)2r = GM/r2 → T2 = (4π2/GM) r3 There may be some property of ellipses such that it becomes clear, perhaps using K2, that the period depends on the semi-major axis but not on the eccentricity.
See also The Geometry of Ellipses, Orbital speed, etc.
For a given heavy primary of mass M, use notation as above, plus ξ = radial velocity and ζ = perpendicular velocity, so that ξ2 + ζ2 = V2.
A. For a given light secondary of mass m :-
i. ½V2 - GM/r =
E/m = -W , energy E is conserved.
ii. rζ =
Q/m = A , angular momentum Q is conserved.
For a bound secondary, E < 0.
B. For different light secondaries :-
i. In circular orbits, V2 = GM/r ;
the square of the speed is proportional to the primary mass and
inversely proportional to the radius. That matches K3 as above.
Consider the situation with a lighter primary, moving significantly about the barycentre.
From A.i and A.ii above .......
For maximum and minimum radii, where
ξ = 0 A = rζ and
W = GM/r - ζ2/2 from above,
W =
GM/r - ½A2/r2
→ 2Wr2
- 2GMr + A2 = 0
so r = ( +2GM ±
(4G2M2 - 8WA2)½ ) / 4W
Dr Robert Matthews, in the Sunday Telegraph, 2003-11-23, p.35, reported an assertion given by Prof Carl Murray (U of London) regarding the Moon that implies that the angular velocity of a secondary about the empty focus of its elliptical orbit is constant. That could be true; but if so I would expect it to be well-known.
Mail from Dr Matthews enclosed a copy of the calculation, which shows the result to be applicable to first (and, I think, second) order in the eccentricity; it is thus practically, but not perfectly, true. All is explained.
That seems to be the correct term for saying that, under some circumstances, it is better to use fuel deep inside a gravity well.
Fuel provides ΔV, and a given ΔV provides a greater change of energy when applied at higher V.
A Hohmann transfer is the most efficient way of changing from one orbit around a primary body to another orbit around that body using just an initial and a final impulse, when the fields of other bodies are negligible. But see Lagrange Point Transfers.
A Hohmann path is an ellipse tangential to the initial and final orbits; see NASA's Hohmann Transfer & Plane Changes.
Here, the initial and final orbits will be taken as circular, to simplify calculation.
The semi-major axis of a Hohmann transfer orbit T is the sum of the initial orbit radius r and the final orbit radius R. From above, r + R = GM/WT where WT is the energy per unit mass which must be added to escape to infinity from the transfer orbit.
The initial circular orbit is essentially a Hohmann orbit between itself and itself, so 2r = GM/Wr (and likewise for the final orbit).
Expression A.i above gives for the insertion velocity
½VT2 - GM/r + WT
= 0
Substitute the previous expression and then from B.i
GM = Vr2r
That soon gives
VT =
Vr √ (2(1 - 1/(1+R/r)))
Particular cases are R = 0, R = r, R = ∞, for which that gives VT = 0, VT = Vr, VT = Vr√2, as it should.
I understand that it is not worth doing an inwards Hohmann in order to use Oberth unless the intent is to escape the system with considerable speed remaining.
For simple escape, it would clearly be ineffective; energy is spent on reaching a lower orbit from which it is harder to escape.
For very high final speed, the effect is small in proportion to the total energy needed.
The semi-major axis of a Hohmann transfer ellipse between two
circular orbits is the average of those of the two orbits. The transfer
time is therefore :-
½ ( ( ½ ( T12/3 +
T22/3 ) )3/2 )
where T1 and T2 are the periods
of the circular orbits.
In particular, T1 = T2 = T
gives a result of ½T, and T2 = 0 gives
a result of
½5/2T ~ 0.177T.
See also in Gravity 3.
This form evaluates interplanetary round trips, to find the minimum total interplanetary flight time. Trips start and finish on Planet 0 = Earth and visit each of the other planets in turn, using Hohmann transfer between planetary orbits. All possible sequences are considered.
The planetary orbits are taken as being circular and co-planar. For bi-Hohmann, in which each stage goes via the Sun, the size of the Sun is taken as negligible.
Using too many planets takes a long time (factorial N or more), especially with Details checked, start with five.
The calculations below assume that the mass of the secondary is negligible in comparison with that of the primary, and hence that the primary has a fixed position. When the masses are comparable, it may be easiest to consider each as rotating about the mutual centre of gravity, under the influence only of a fictitious body located there with a mass giving the correct field.
For each Form, enter the figures (which can be expressions), then use the button.
The speed and acceleration of a body in a circular path of radius R and period T are most simply obtained as ωR and ω2R where ω = 2π/T.
For bodies orbiting our Sun, period in years equals semi-major axis in AU to the power 3/2.
The "Artificial" periods, at least, are approximate.
The gravitational field at a distance R from a body of mass M is GM/R2, and, for the circular speed, V2 = GM/R, where G = 6.673E-11 in SI units (CODATA 1998).
GSO* has had the mass adjusted for the correct distance and period, assuming the given G; the period is siderial.
For an elliptical orbit, the period varies only with the primary mass and the semi-major axis; so use the latter as the radius in the above.
From expressions above, the period T is
2 π R / √ (GM/R)
and M is 4/3 π ρ R3,
thus T2 = 4 π2 R2 R /
(G 4/3 π ρ R3) =
3 π / G ρ ;
for the Earth, ρ = 5517 kg/m3
giving T = 5060 s = 1h,24m,20s.
This was page $iss.htm.
For an orbiting body one can determine, from the period and the rate at which the height decreases, the force (per unit mass) and acceleration due to atmospheric drag.
Consider a body of mass M in a circular orbit of present radius R and period T, decaying from a small drag force F :-
Kepler's Third Law : T2 = k R3
Orbital Speed :
V = 2 π R / T = 2 π / √ (k R)
dV/dt = - π /
√ (k R3) dR/dt =
- ( π / T ) dR/dt
Since dR/dt is negative, that represents an increasing speed.
Kinetic Energy : X = 0.5 M V2
As escape speed is √2 times circular speed, total energy
E = - X (zero for stationary at infinity)
→ V2 =
4 π2 R2
/ T2
= 4 π2 / k R
→ E =
- 2 π2 M / k R
→ dE/dR =
+ 2 π2 M / k R2
dE/dt = -F × V = - 2 π F R / T
dR/dt = dE/dt / dE/dR =
( - 2 π F R / T ) / ( 2 π2 M / k R2 )
= - F/M k R3 / π T =
- F/M T2 / π T = - F/M T / π
Thus : F/M = - ( π / T ) dR/dt : units are newtons/kilogram or metres/second2.
The speed increases at the same rate as the drag alone would decrease it.
I have read that the thrust of NASA's Deep Space 1 was 0.09 N.
See also Wikipedia Asteroid deflection strategies currently leading to Gravity tractor & Gravitational tractor.
The paper A Gravitational Tractor for Towing Asteroids by Edward T. Lu and Stanley G. Love (148kB PDF) discusses a non-orbiting tractor with canted thrusts. An orbiting tractor makes more efficient use of its thrust, but less efficient use of its mass.
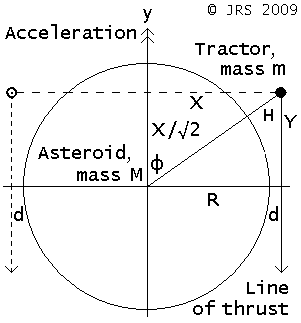
The Dynamics of an Asteroid which is orbited by a mass thrusting in a constant direction are partly indicated in Wikipedia, Gravity tractor.
This treatment deals with the ideal case, ignoring practical minor inefficiencies such as spreading of the exhaust may cause.
Consider a spherical asteroid of mass M and radius R to be towed in the +y direction by a tractor of much smaller mass m orbiting round the y axis through Cartesian position (X = R+d, Y, 0) and thrusting in the -y direction.
Attraction of the asteroid by the tractor : F = G M m / (X2 + Y2) Cosine φ : C = Y / √ (X2 + Y2) Attraction resolved along +y : F×C = G M m Y / (X2 + Y2)3/2
That is maximum when (X2 + Y2)3 / Y2 is minimum, which is at Y = X/√2 (φ≈55°), where F×C = G M m X/√2 1/(X2 + X2/2)3/2 so the acceleration A of the asteroid is : F×C / M = 2 G m / 33/2 X2 and the required thrust is of course (M+m)×A.
The wobble radius of the asteroid's course will be about Xm/M.
The period of the orbit will depend only on the density of the asteroid, and will be a little greater than that given in Lowest Orbit Time, given the Primary Density above.
The surface gravity field of the asteroid is GM/R2. For a tractor at height H = X√1.5 - R, the tractor's field at its nadir is Gm/H2.
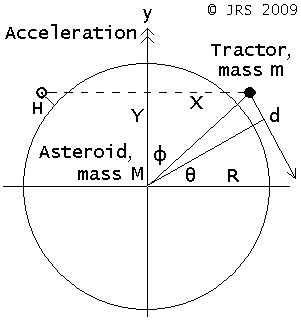
The obvious placing of the orbiting tractor is as above - at a radius such that, firing aft, the exhaust just misses the asteroid surface (distance d allows for the spread). However, that cannot be optimum, unless it is necessary to mimimise fuel use : if the exhaust is directed slightly outwards at an angle θ, there is a second-order effect on the towing efficiency, but the tractor can be moved inwards by a first-order amount which has a first-order effect on the towing force, to increase the acceleration of M provided by a given mass m.
Consider a spherical asteroid of mass M and radius r at Cartesian position (0, 0, 0), to be towed in the +y direction by a tractor of much smaller mass m orbiting round the y axis and currently crossing z=0. Let the tractor exhaust be canted outwards at an angle θ to the -y direction, with its centre-line. passing within distance d from the surface. The thrust is therefore tangential to the surface of radius R = r+d.
By adding a second tractor orbiting at 180° from the first and then allowing angle φ to become zero, the essentials of the Lu and Love proposal are recovered.
Selecting the optimum θ is a trade-off between use of fuel and use of mass, and is beyond the scope of this page.
The thrust will pass through position (Rcosθ, Rsinθ, 0). The tractor m will be on that line of thrust, at (Rcosθ - ksinθ, Rsinθ + kcosθ, 0). The need is to optimise the attraction by varying k for a given θ.
Field at the asteroid from the tractor : F = G m / (X2 + Y2) The cosine and sine of φ : C = Y / √ (X2 + Y2) , S = X / √ (X2 + Y2) Acceleration field resolved along +y : A = F×C = G m Y / (X2 + Y2)3/2
The required thrust should be (M+m)×A / C.
Period = 2π/ω ; ω = √ (f/o) ; f = F×S + thrust× ...
Since fuel has mass, the optimum θ is likely to vary during the mission. Also, the benefit of acceleration must be greater at the beginning. Overall optimisation is non-trivial.